
Zadanie Gra (gra)
Pomóż nam usprawnić bazę zadań!
Gra
Limit pamięci: 32 MB
Rozważmy grę na prostokątnej planszy 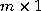 złożonej
z
złożonej
z 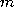 jednostkowych kwadratów ponumerowanych kolejno od
jednostkowych kwadratów ponumerowanych kolejno od  do
do 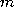 .
Na planszy ustawionych jest
.
Na planszy ustawionych jest  pionków, każdy na innym polu, przy
czym żaden pionek nie znajduje się na polu o numerze
pionków, każdy na innym polu, przy
czym żaden pionek nie znajduje się na polu o numerze 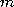 .
Pojedynczy ruch w grze polega na przestawieniu dowolnie wybranego
pionka na pierwsze wolne pole o większym
numerze.
Dwaj gracze wykonują na zmianę po jednym ruchu.
Wygrywa ten, który postawi pionek na ostatnim polu,
tzn. na polu o numerze
.
Pojedynczy ruch w grze polega na przestawieniu dowolnie wybranego
pionka na pierwsze wolne pole o większym
numerze.
Dwaj gracze wykonują na zmianę po jednym ruchu.
Wygrywa ten, który postawi pionek na ostatnim polu,
tzn. na polu o numerze 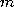 .
.
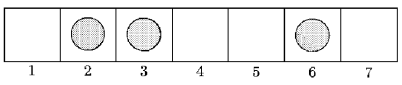
Dla przykładu z rysunku (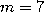 ), gracz
może wykonać ruch z pola
), gracz
może wykonać ruch z pola 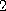 na
na  , z pola
, z pola 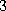 na
na  lub z pola
lub z pola 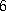 na
na 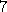 .
Ten ostatni ruch kończy grę.
.
Ten ostatni ruch kończy grę.
Mówimy, że ruch gracza jest wygrywający, jeżeli po jego wykonaniu gracz ten może wygrać grę niezależnie od tego, jakie ruchy będzie wykonywał jego przeciwnik.
Zadanie
Napisz program, który:
- wczyta ze standardowego wejścia rozmiar planszy i początkowe rozstawienie pionków,
- wyznaczy liczbę różnych ruchów wygrywających, jakie w zadanej sytuacji początkowej ma do wyboru gracz rozpoczynający grę,
- wypisze wynik na standardowe wyjście.
Wejście
Pierwszy wiersz wejścia zawiera dwie liczby całkowite
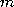 i
i  (
(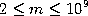 ,
, 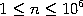 ,
, 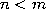 )
oddzielone pojedynczym odstępem.
Drugi wiersz zawiera
)
oddzielone pojedynczym odstępem.
Drugi wiersz zawiera  rosnących numerów pól, na
których znajdują się pionki. Liczby w wierszu są
pooddzielane pojedynczymi odstępami.
rosnących numerów pól, na
których znajdują się pionki. Liczby w wierszu są
pooddzielane pojedynczymi odstępami.
Wyjście
Pierwszy i jedyny wiersz wyjścia powinien zawierać liczbę różnych ruchów wygrywających, jakie może wykonać w zadanej sytuacji początkowej gracz rozpoczynający grę.
Przykład
Dla danych wejściowych:
5 2 1 3
poprawną odpowiedzią jest:
1
a dla danych wejściowych:
5 2 2 3
poprawnym wynikiem jest:
0
Autor zadania: Bartosz Walczak.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English